Understanding the carbonic acid/bicarbonate buffer in hydroponics
I have written several articles before about pH and it’s importance in hydroponic culture (1, 2, 3, 4). However I have yet to write a detailed explanation of one of the most important buffering systems in hydroponics, which is the carbonic acid/bicarbonate buffer. This buffer is significantly more complicated than the simpler buffer created using phosphoric acid species, as it not only relies on ions present in solution but also on the partial pressure of carbon dioxide in the atmosphere. In this article I will attempt to explain this buffering system in detail, shining some light into the limitations of this buffer and how changing different key variables can fundamentally affect the way it works in hydroponics.
A buffer is nothing more than a pair of chemical species in solution that are present at a certain pH, that can react with additional H3O+ or OH- ions that are introduced into the solution. Since these ions control the value of pH, anything that prevents their concentration from changing will keep the pH stable. Distilled water, for example, has absolutely no buffering capacity since within it there is nothing that can react with incoming H3O+ or OH– ions that are added to the solution. Distilled water should therefore have a pH of 7.0, it does not because we live in an environment where an acid can always be generated from the air. This acid – carbonic acid – is generated in water whenever it’s put into contact with a carbon dioxide containing atmosphere. This makes distilled water have a pH of around 5.6.
To be able to calculate the pH we need to consider all the chemical equilibrium reactions that happen, these are summarized here and in the image above. We must consider that carbon dioxide will dissolve in water to always satisfy Henry’s law, that dissolved carbon dioxide will be in equilibrium with carbonic acid, that carbonic acid can dissociate into a H3O+ ion and a bicarbonate ion and that a bicarbonate ion can further dissociate into an additional H3O+ ion and a carbonate ion. To solve all of this we must also consider that charge neutrality must be preserved, meaning that the sum of all molar charges of all positive ions must be equal to the molar charges of all negative ions. To carry out these calculations I routinely use the freely available Maxima software. Below you can see the code I use to solve this system in Maxima (constants are taken from here):
[kw : 10^(-14.0), kh: 1.7*10^(-3.0), kc1: 2.5*10^(-4.0), kc2: 4.69*10^(-11.0), co2: 1.32*10^-5]; log10(x) := log(x)/log(10) ; pH(x) := float(-log10(x)); float(solve([h*oh=kw, h = 2*co3+hco3+oh, kh=h2co3/co2, kc1=(hco3*h)/h2co3, kc2=(co3*h)/hco3],[oh, co3, hco3, h2co3, h]));
This is the solution obtained for the molar concentrations (rounded for clarity): oh = 4.21*10^-9 co3 = 4.68*10^-11 hco3 = 2.36*10^-6 h2co3 = 2.24*10^-8 h = 2.37*10^-6
After executing this code you will get several different possible solutions, but the only one that interests us is the one where the H3O+ (h) concentration is a positive number (this solution is showed above). We can then use the pH function to calculate the value of pH for this H30+ concentration, which gives us a value of 5.62, this matches the real measurement of a distilled water solution at 25C under a 387ppm carbon dioxide atmosphere. Note that the amount of none dissociated acid in solution is very small. Taken to mass, the concentration of carbonic acid is 0.00138 ppm. However the concentration of bicarbonate is significantly greater, at 3.6 times the concentration of undissociated carbonic acid. This explains why the pH drops so much, since a significant amount of the generated carbonic acid ends up dissociating and contributing H3O+ ions to the solution. This also shows you how little acid is needed to drop the pH of an unbuffered solution.
To create the buffer with the biggest possible strength we would need to add enough strong base to shift the pH to the point where the pH equals the pKa (which is just -Log(equilibrium constant)) of the joint reactions created from the reaction of carbon dioxide with water to create carbonic acid and the subsequent dissociation of this acid into bicarbonate and H3O+. This point is at 6.3 under atmospheric conditions at 25C. This can be achieved with the code below:
[kw : 10^(-14.0), kh: 1.7*10^(-3.0), kc1: 2.5*10^(-4.0), kc2: 4.6910^(-11.0), co2: 1.32*10^-5, h:10^(-6.3)]; float(solve([hoh=kw, base+h = 2co3+hco3+oh, kh=h2co3/co2, kc1=(hco3h)/h2co3, kc2=(co3h)/hco3],[oh, co3, hco3, h2co3,base]));
This is the solution obtained for the molar concentrations(rounded for clarity): oh = 1.99*10^-8 co3 = 1.04*10^-9 hco3 = 1.11*10^-5 h2co3 = 2.24*10^-8 base = 1.07*10^-5
The pH here is set to 6.3 and we can see that to get there we would need to add a base at a concentration of 1.07*10-5.0. If this base was KOH this would imply adding it at a rate of 0.6 ppm. We can see how the pH changes as a function of adding base or acid from this point. If at this point we decided to double the addition of strong base we would get to 6.57, tripling it would take us to 6.73 and adding 10 times more base would take us to 7.25. The buffer is indeed resisting the increase in pH by basically drawing CO2 from the air to react with the incoming base as base is added to the solution. However you might notice that under equilibrium conditions the buffering capacity of this system is very low. Just 6 ppm of a KOH equivalent strong base addition can strongly affect the pH – taking it from 5.6 to 7.25 – so how can the carbonic acid/bicarbonate buffer be effective at all in hydroponics?
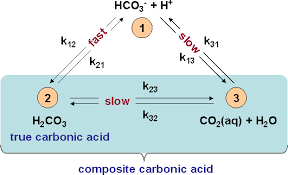
The answer is in the first image in this post. The equilibrium reaction between carbonic acid and water plus carbon dioxide in water (k23/k32) is fundamentally slow. We can take advantage of this by generating larger amounts of carbonate species in solution through the use of exogenous carbonate or bicarbonate additions and then setting the pH at a lower value to generate more carbonic acid, this acid will then take some significant time to reach equilibrium. This is the reason why using tap water with a significantly high alkalinity can provide a surprisingly stronger buffer than what would be expected at equilibrium and it also has some interesting consequences in the use of nutrient solutions.
Let’s consider a case where there is no decomposition of carbonic acid – let’s suppose it’s extremely slow – and say we add 100 ppm of potassium carbonate into a solution and then set the pH back to 5.8 using phosphoric acid. In this case the predominant reactions in solution would be the dissociation of dihydrogen phosphate to hydrogen phosphate and H3O+ and the carbonic acid dissociation discussed before. In order to properly consider this case we must also introduce two additional equations, mainly the mass balance equations for the phosphate and carbonate species, since this time we are assuming no carbon dioxide is ever lost to the atmosphere. Note that I have changed the equilibrium constant for the carbonic acid reaction here to 10-6.3 where carbonic acid is now “apparent carbonic acid”. You can see the equation system and solution below:
[kw : 10^(-14.0), kh: 1.7*10^(-3.0), kc1: 10^-6.3, co2: 1.32*10^-5, kp:10^-7.2, total_p: 1.7*7.2310^-4, total_c: 7.23*10^-4]; float(solve([h*oh=kw, total_c=hco3+h2co3, total_p=h2po4+hpo4, 2*total_c+h = hco3+oh+h2po4+2*hpo4, kc1=(h*co3h)/h2co3, kp=(hpo4*h)/h2po4],[hco3, h2co3, h2po4, hpo4, h, oh]));
This is the solution obtained for the molar concentrations(rounded for clarity): hco3 = 1.72*10^-4 h2co3 = 5.50*10^-4 h2po4 = 0.00118 hpo4 = 4.64*10^-5 h = 1.60*10^-6
The final pH of this solution is very close to 5.8 and the concentration of P is 47.9 ppm with K at 38.10 ppm. Notice however that apparent carbonic acid has a concentration of 5.50*10-4 M, which implies that the system is not at equilibrium since this amount is significantly larger than what we would expect from Henry’s law. If we reduce the concentration of carbonic acid to half then the pH will increase to 6.01, as we would expect from extracting an acid from the solution. The implication is that – with time – the pH of this solution is going to slowly increase, as carbonic acid decomposes and the solution reaches an equilibrium with the atmospheric carbon dioxide level. This is also why nutrient solutions that are prepared with tap water high in carbonates and then aerated will tend to show a rapid increase in pH – even if the solution is not fed to plants – as the reaching of equilibrium is accelerated by the agitation of the solution and the contact with air (that allows CO2 in solution to escape).
As soon as the above solution is prepared it offers a substantially superior buffering capacity when compared with a solution containing only phosphates. This is why water with high alkalinity tends to provide better pH stability in drain to waste type systems when compared with solutions prepared with RO water. This water contains a significant amount of carbonates that are turned into carbonic acid and bicarbonate as soon as the pH is lowered to the pH range used in hydroponics. As long as the solution is used quicker than the carbonic acid decomposes, there will be a substantial increase in pH stability.
If you are using RO water or water with low alkalinity to prepare your solutions you can obtain a similar effect by adding 100-200 ppm of potassium carbonate before you start preparing the nutrient solution, you can similarly use bicarbonate but I would recommend using potassium carbonate, as it is cheaper. It would also be advisable to use the solution as fast as possible, since time will cause the solution to reach equilibrium and the pH to increase. This effect will take much longer if the CO2 concentration is higher – which is true for setups that use enriched CO2 – or if the temperature is lower, which increases the solubility of CO2.